How to Design Two Way Slab using Coefficient Method

Let's look into steps on how to use the coefficient method to design a Two Way Slab. All we need is to get the moment coefficients from provided table here to solve for moments along top and bottom bars both for the short and long span. 

Before that we must first get the ratio and type of case needed. Get a quick read on this post here to get an idea how two way slab differ vs one way slab.

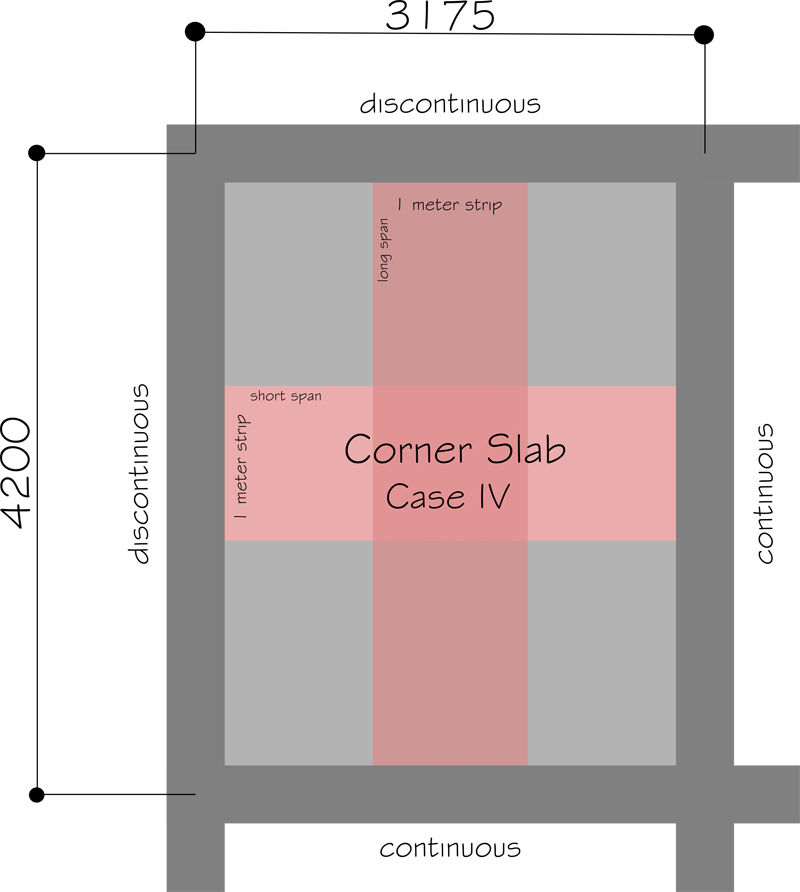
Given problem:

• corner slab
• W=3175mm (center to center of beam)
• L=4200mm (center to center of beam)
• f'c=21 mPa
• fy=228 mPa
• use bar diameter=10mm ⌀
• concrete density=24 kN/cu.m
• Liveload=2 kPa
• superimposed Deadload=4 kPa

SOLUTION:

1. Get m ratio 

★ where la and lb are clear span of slab

★ if no width of beam provided, just deduct 100mm on both sides to get clear span

m(ratio) = (3175-200)/(4200-200)

              = 0.743 round to nearest increments of 0.05 as per table (here)

              = 0.75

2. Check CASE

★ verify plans on slab if interior, corner etc

★ since problem mentioned slab as corner, then it will fall under case IV (two adjacent sides are discontinuous)

★ look into three tables and get all coefficients under case IV with 0.75 ratio

Table 1 Coefficient of Negative Moments in Slab

Table 2 Coefficients for Dead Load Positive Moments in Slabs

Table 3 Coefficients for Live Load Positive Moments in Slabs

summary:

Ca,neg         0.076      Cb.neg         0.024

Ca,DLpos    0.043      Cb.DLpos    0.013

Ca,LLpos    0.052      Cb.LLpos     0.016

3. Compute for minimum slab thickness & effective depth

★ since no given slab thickness we may use the formula 

h=perimeter/180

= [2*((3175-200)+(4200-200))]/180

= 77.50mm

or this formula (source: here)

where B is your longer clear span (=4200-200), and β is 1/m (m=0.75) = 1/0.75 = 1.333

= [(4200-200)*(0.8+(228/1400)]/(36+9(1.333))

= 80.24 mm

★ both are less than 90mm so we can assume 100mm (0.10m) as slab thickness for the design or higher.

Now solve for d (effective depth)

★ some use one effective depth for both spans

★ others compute two separate "d" for short and long span respectively

Solving for "d"

★slab thickness less concrete cover less half of your bar diameter

★20mm concrete cover for slabs unless exposed to extreme conditions (check here)

"ds" for short span

=100-20-(10/2)

=75mm

"dl" for long span

=100-20-(10⌀/2)-10⌀

=65mm

4. Compute for the Dead load, Live Load and ultimate

★ for computation we will only consider a 1meter strip of the slab

a. DL=24kN/m³ * 0.10m

         =2.4kN/m² + 4kN/m²

         = 6.4kN/m² or 6.4kPa

b. LL= 2kN/m² or 2kPa

c. ⍵u = 1.2DL + 1.6LL

          = 1.2(6.4kPa) = 7.68kPa

          = 1.6(2kPa)    = 3.20kPa

total ⍵u = 10.88 kPa

5. Compute for Moments for Short & Long span

★ where Mu=c⍵l²

★ where l is the clear span

★ where ⍵ is your load

a. Solving for Mu @ Short Span

where l=(3175mm - 200mm) = 2975mm or 2.975m

for Top bars

Mu,neg = 0.076*10.88kN/m²*2.975m²

             = 7.318 kN x 1m strip

             = 7.318 kN-m ✓

for Bottom bars

Mu,pos = (0.043*7.68kN/m²*2.975m²) + (0.052*3.20kN/m²*2.975m²)

             = 4.396 kN x 1m strip

             = 4.396 kN-m ✓

b. Solving for Mu @ Long Span

where l=(4200mm - 200mm) = 4000mm or 4m

for Top bars

Mu,neg = 0.024*10.88kN/m²*4m²

             = 4.178 kN x 1m strip

             = 4.178 kN-m ✓

for Bottom bars

Mu,pos = (0.013*7.68kN/m²*4m²) + (0.016*3.20kN/m²*4m²)

             = 2.417 kN x 1m strip

             = 2.417 kN-m ✓

6. Solving for rho (ρ)

★ use flexure formula

where Mu=your computed moment

𝝓=reduction factor of 0.90

b=1 meter strip or 1000mm

d=effective depth (refer to step #3)

solve for 𝛚

solve for rho (ρ) once you get your 𝛚

a. Solving for (ρ) @ Short Span

Mu,neg = 7.318 kN-m ✓ top bars

Mu,pos = 4.396 kN-m ✓ bottom bars

7.318 kN-m x 10⁶ ≤ 0.90*21*1000*75²𝜔(1-0.59𝜔)

𝜔=0.07188

ρ=(0.07188*21)/228 = 0.00662

compare with ρmin=1.4/fy

♦ ρmin=1.4/228 = 0.00614 

ok ρ>ρmin, use ρ=0.00662 ✓

4.178 kN-m x 10⁶ ≤ 0.90*21*1000*75²𝜔(1-0.59𝜔)

𝜔=0.04026

ρ=(0.04026*21)/228 = 0.00371

compare with ρmin=1.4/fy

♦ ρmin=1.4/228 = 0.00614 

not ok ρ<ρmin, so use ρmin=0.00614 ✓

unless you want to use the 4/3 of your computed ρ which is allowed by ACI 

= (4*0.00371)/3 = 0.00495 

7. Solving for Area of Steel (As)-main bars

★ use As=ρbd

★ where ρ must be ≧  ρmin (from step #6)

a. Solving for (As) @ Short Span

ρuse=0.00662 top bars

ρuse=0.00614 bottom bars

As=0.00662*1000*75 = 496.50 mm² for main bars

As=0.00614*1000*75 = 460.50 mm² for main bars

Must not be lesser than As of temperature bars

Checking for As(minimum) of temp bars

fy lesser than 420mPa

Asmin=0.002bh = 0.002*1000*100 = 200mm

★computed values for As(main bars) are greater than Asmin of temp bars, so ok ✓

8. Solving for Spacing of Steel (S)

★ use S=(A⌀/As)*b

★where A⌀=𝝅r² or A⌀=𝝅d²/4

★ where b = 1 meter strip or 1000mm

 

a. Solving for (S) @ Short Span

As = 496.50 mm²

As = 460.50 mm²

S=[(𝝅5²)/496.50]*1000 = 158mm or 150mm (round to nearest 25 if possible)

S=[(𝝅5²)/460.50]*1000 = 170mm

Checking for minimum and maximum allowed

Smin=50mm, db, 4/3 dagg whichever is higher

★computed value for S is greater than minimum, so ok ✓

Smax=3h or 450 = 3(100) = 300 or450 

★we get the minimum of the two which is 300mm as Smax

★computed value for S is lesser than Smax, so ok ✓

Therefore:

♦ Top bars spacing 150mm 

♦ Bottom bars spacing 150mm (we adapt the least spacing to be uniform)

Just to make sure that the design is Tension Controlled Section, we must have 𝜀t≧0.005

We first need to solve for ∝

∝ = (496.50*228)/(0.85*21*1000) =  6.34

∝ = (460.50*228)/(0.85*21*1000) =  5.88

Solving for c

where 𝛽 =0.85 since f'c is ＜ 28 mPa

c = 6.34/0.85 = 7.45

c = 5.88/0.85 = 6.92

Solving for 𝜺

soluton:
𝜀= [(0.003*(75-7.45)]/7.45 = 0.027 ＞0.005 ok, Tension Controlled!

𝜀= [(0.003*(75-5.88)]/5.88 = 0.035 ＞0.005 ok, Tension Controlled!

Designers always want to have it "Tension Controlled" where steel will yield first or will fail first before concrete to give ample time of warning before a structure may collapse.

What we have shown you is the rebar spacing along short span, follow same process and solve for the spacing for the long span to practice.

Check from Download section for calculator for your use, make sure to compare with your own computations.

Hope this post helps you in your design.

Make sure to share with friends if you find this helpful! Cheers!